rossler混沌系统,复杂性中的秩序

探索Rossler混沌系统：复杂性中的秩序

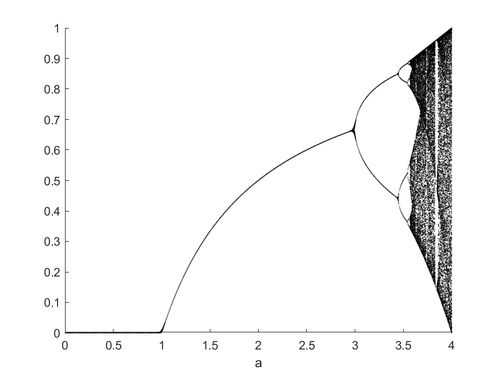
混沌理论是研究确定性系统中出现的看似随机行为的科学。在众多混沌系统中，Rossler混沌系统因其独特的动力学特性和丰富的应用场景而备受关注。本文将深入探讨Rossler混沌系统的基本原理、特性及其在各个领域的应用。

什么是Rossler混沌系统？

Rossler混沌系统是由德国物理学家Ottmar Rossler在1976年提出的一个三维自治微分方程系统。该系统由以下方程组描述：

dx/dt = -y - z

dy/dt = x + ay

dz/dt = b + z(x - c)

其中，a、b、c是系统参数，x、y、z是系统状态变量。

Rossler系统的特性

Rossler混沌系统具有以下特性：

1. 超混沌：Rossler系统具有两个正的Lyapunov指数，表明系统具有比一般混沌系统更复杂的动力学行为。

2. 对称性：系统具有关于x轴的对称性，即当x=0时，系统状态保持不变。

3. 吸引子：系统存在一个吸引子，即系统状态在长时间演化后趋向于一个稳定的状态。

4. 分岔：系统参数的变化会导致系统行为的显著变化，如从周期运动到混沌运动。

Rossler系统的应用

Rossler混沌系统在多个领域都有广泛的应用，以下是一些典型的应用场景：

1. 天气预报：混沌理论在天气预报中具有重要意义，Rossler系统可以模拟大气中的一些复杂现象。

2. 生物医学：在生物医学领域，Rossler系统可以用于模拟心脏、神经元等生物系统的动力学行为。

3. 通信系统：混沌通信技术利用混沌系统的特性实现信号的传输，提高通信系统的安全性。

4. 图像加密：混沌系统可以用于图像加密，提高图像传输的安全性。

控制Rossler混沌系统

由于混沌系统的敏感性，控制混沌系统成为了一个重要的研究方向。以下是一些控制Rossler混沌系统的方法：

1. 比例微分控制器（PDC）：通过调整系统参数，使系统状态趋向于期望的稳定状态。

2. 模糊PID控制：利用模糊逻辑技术，实现混沌系统的自适应控制。

3. 混沌同步：通过同步两个混沌系统，实现混沌控制的目的。

Rossler混沌系统是一个具有丰富动力学特性的混沌系统，其在各个领域的应用为混沌理论的研究提供了新的视角。随着混沌理论研究的不断深入，相信Rossler混沌系统将在更多领域发挥重要作用。